Filters, Phase, and the Double Patched Kick

This post comes on the heels of this article by my friend Jim Yakabuski, and my recent article about double-patched channels, so if you’re not up to speed on those, check them out and then come back. I’ll be here.

 

Back? Okay great.

So the discussion now is that we want to split a kick mic into “Kick Low” and “Kick Hi” and there are several ways to accomplish that. In general, our major concern is phase problems, and so we take the following strategy:

1. If one channel has a clear level advantage (>10 dB) at a given frequency, we don’t have to worry about phase, because the quieter signal can’t significantly effect the summation.
2. If both channels are at a similar level in a given frequency range, they should also be in phase with each other. (If we’re within about 50°, we’ll have an effectively full summation. Trouble sets in past 120°.)

What if we just double patch the input into two channels, and boost LF on on and HF on the other? Some folks (including myself until an hour ago) would find this alarming, because without measuring it, you’d say “well, we have two signals both contributing energy at the same frequency at similar levels, but the EQ will cause phase shift on one of them. Oh no!”

But when measured:

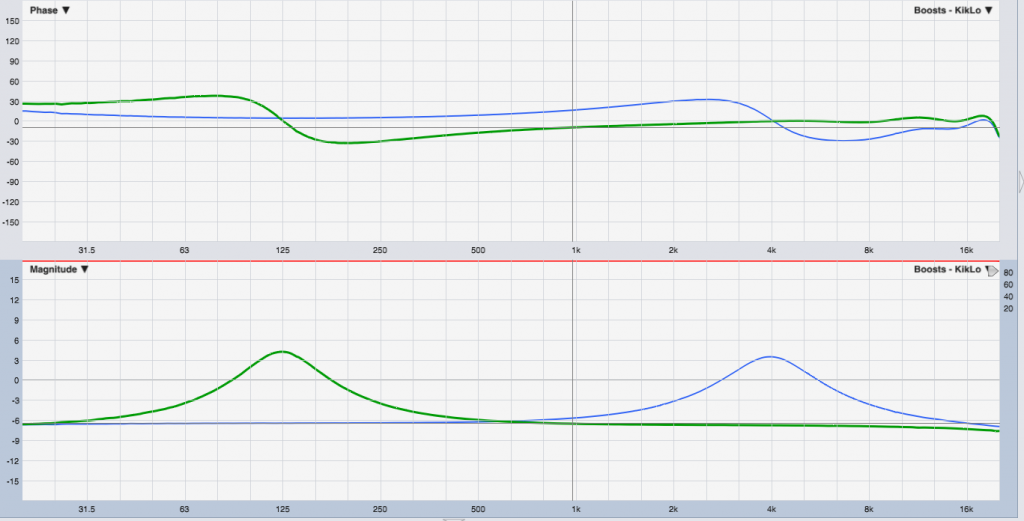
Yeah, that’s nothing to write home about.

Let’s add in the summation of the two when mixed together (in red):

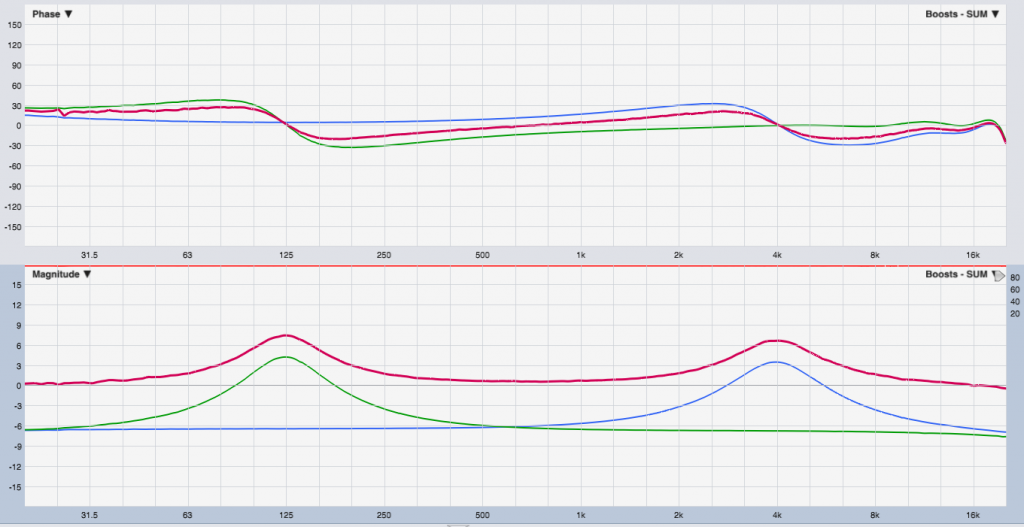
Notice the result is up 6 dB from the individuals for most of the range (summation of equals).

Let’s look at a different method: a low-pass on one side and high-pass on the other.

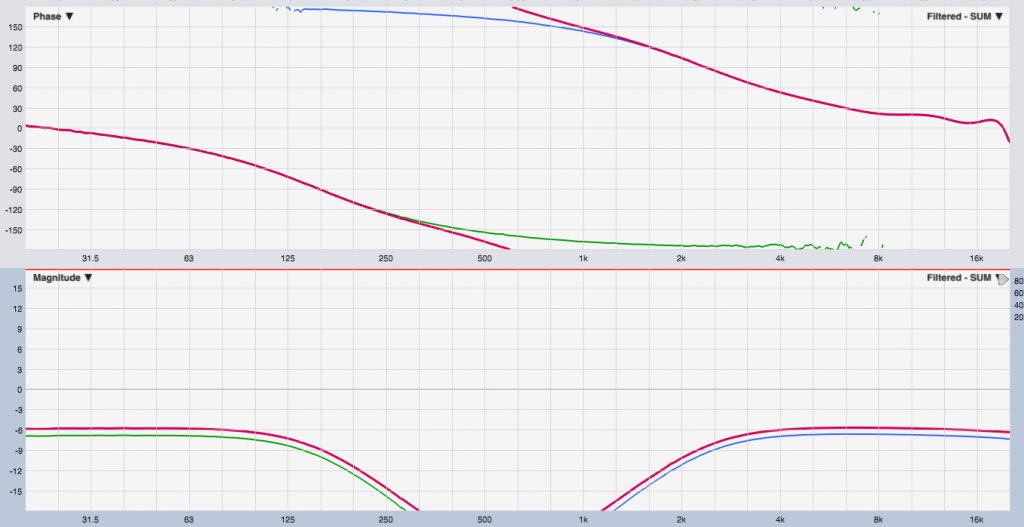
Now we’ve eliminated any overlap between the two bands and so we have a phase response that perfectly matches the individual response in that frequency range. Note that due to the phase shift of the filters, we are a cycle behind up top. We’ll return to that.

What if we combine both approaches, the HPF/LPF and the boosts?

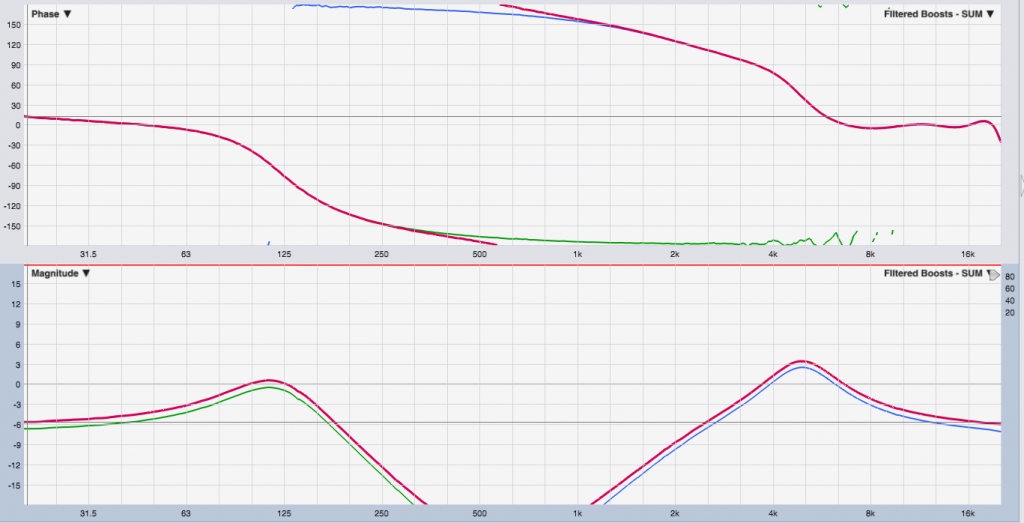
Not really that much different. And, for those familiar with the maths of minimum-phase filters, this is not a surprise.

But let’s talk about time smearing. Let’s see impulse responses for these options:

1. Both filters flat

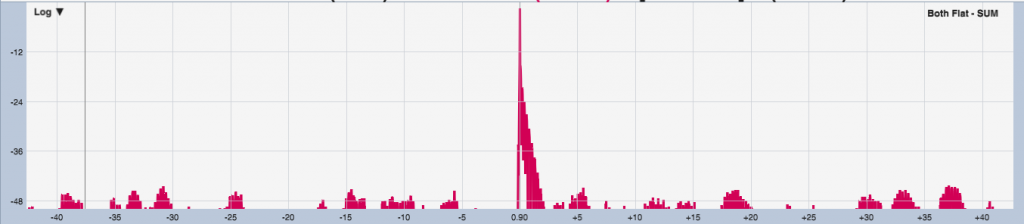
2. The double-patch and boost option:

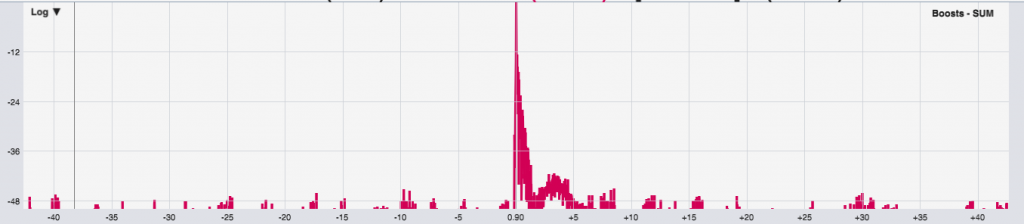
3. The HPF/LPF option:

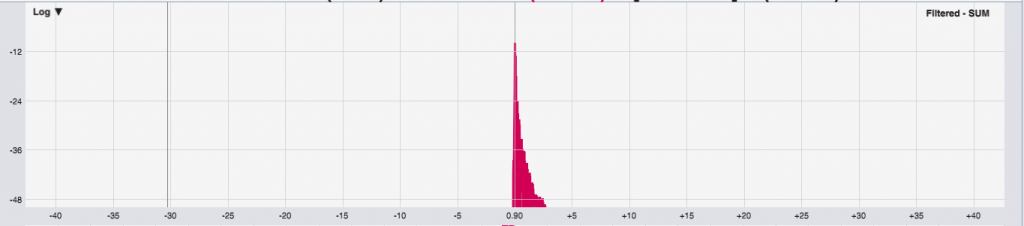
4. And finally, the hybrid (filter and boost):

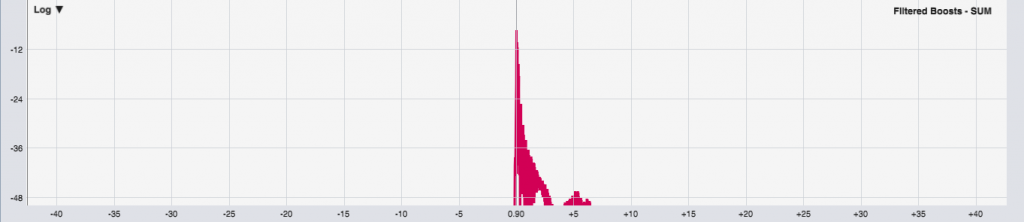
We can see a very slight elongation in the IR decay time with the HPF and LPF options because of the extra cycle added, but it doesn’t look night-and-day to me. That being said, the double-patch-and-boost approach is likely the cleanest result of the options.

What if we can science this a little bit by adding complimentary cuts on one channel where the other is boosted? 

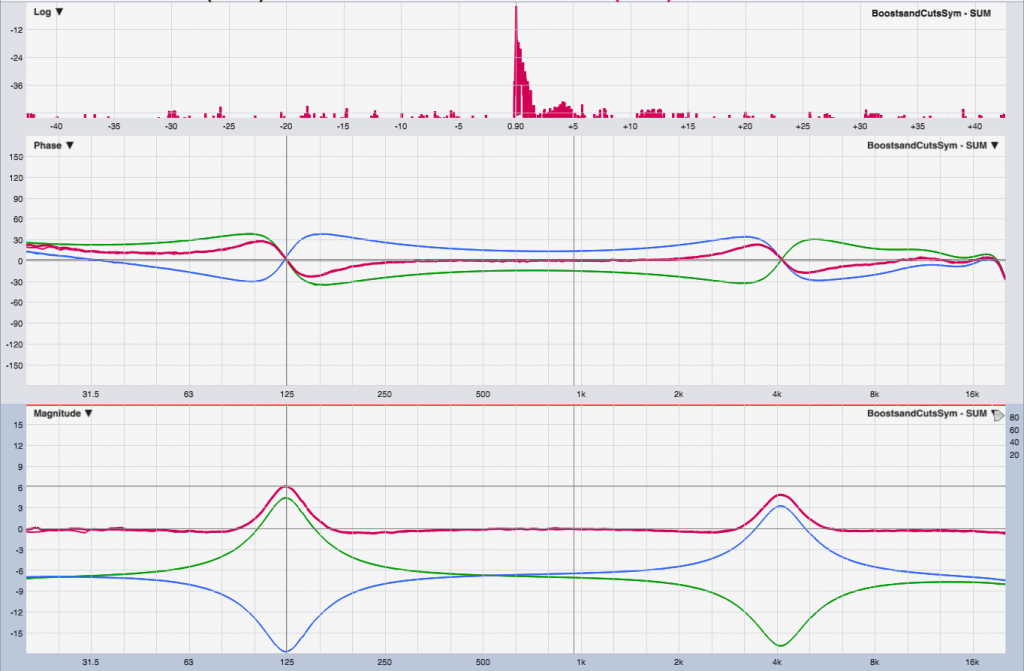
The interesting thing about this approach is that the boosts are not as effective in practice as we would thing. Here, a 12 dB EQ boost results in only about 6 dB boost in the final response. Why? Because we lost the 6 dB that we would have had by having two coherent copies of the same signal, as we do with other frequencies. Since they’re no longer coherent signals matched in level (due to the boost), we lose the 6 dB, and then we gain 12 from the filter boost, so we end up +6 from where we started. 

So if you’re using this method, expect to push the EQs a little harder than you would expect.