Audio Analyzer Mythbusting

The wonderful silver lining of our present situation is that the internet is being flooded with all sorts of seminars, online classes, training videos, and the like. I’ve got a bunch of stuff bookmarked to dive into and it feels a bit like trying to drink from a firehouse. However, I’ve stumbled across a few resources that seem to have some wires crossed regarding measurement theory and audio analyzers so I wanted to take a minute and address some of the common mixups.

“FFT” vs “RTA” vs “Transfer Function”

Several resources seem to conflate these terms. Here’s the scoop: FFT stands for Fast Fourier Transform, which is a mathematical operation that transforms time-domain data into frequency-domain data. In other words, it tells us what frequency components make up a signal.

Regardless of whether you’re looking at an RTA or a Transfer Function measurement in Smaart, the FFT is what’s happening under the hood to generate that data. 

So trying to draw a comparison like “FFT vs RTA” is sort of like saying “Internal Combustion Engine vs Dodge Charger”. What makes a bit more sense to discuss is RTA vs Transfer Function measurements, but both use FFT under the hood.

 

“Frequency Response” vs “Magnitude Response”

The terms “magnitude response” and “frequency response” are often used interchangeably, however this is shorthand and it’s good to be clear on what we really mean, for the sake of the folks who might not know the difference, kinda like that whole phase/polarity thing.

The magnitude response measurement displays magnitude over frequency, and the phase response measurement shows phase over frequency. The phase trace is a frequency-domain measurement as well, so in this context, the term “frequency response” refers to both magnitude and phase over frequency, often displayed in the form of a Bode plot.

 

Data Window Functions

Contrary to some claims, data window functions aren’t used to fix “rounding errors” or “infinitely repeating” decimal values. Here’s the deal: the textbook Fourier transform has a continuous frequency response running from 0 to infinity (DC to light, if you want to think of it that way). However, in order for that to work, T = 1/f tells us that the input signal must also be infinitely long. That’s not going to work too well for our purposes, we have sound check in an hour. So audio analyzers use a Discrete Fourier Transform (DFT) which uses just a chunk of an input signal (which we call the Time Record or Time Window) and assumes that it’s infinitely repeating in a similar fashion. If you listen to a four-bar drum loop in your DAW, you know it will sound the same even if you loop it forever. (“But wait,” you might think. “What’s all this Discrete nonsense? I thought they used Fast Fourier Transforms.” The “Fast” bit is a special version of the DFT that can be calculated more efficiently, which is what allows us to carry out the analysis in realtime. So FFT is just a special flavor of DFT.)

However, the whole “infinitely repeating” bit is an assumption that’s not true with real-world audio signals. If you’ve ever built loops in a DAW, you know the snap/crackle/pop nasties that are created by a bad loop edit. This causes a bunch of noise and error in the measurement that manifests by signal content at one frequency “bleeding” into the other frequency data points. See here how a 500 Hz sine wave spills over into the full spectrum of the measurement bandwidth.

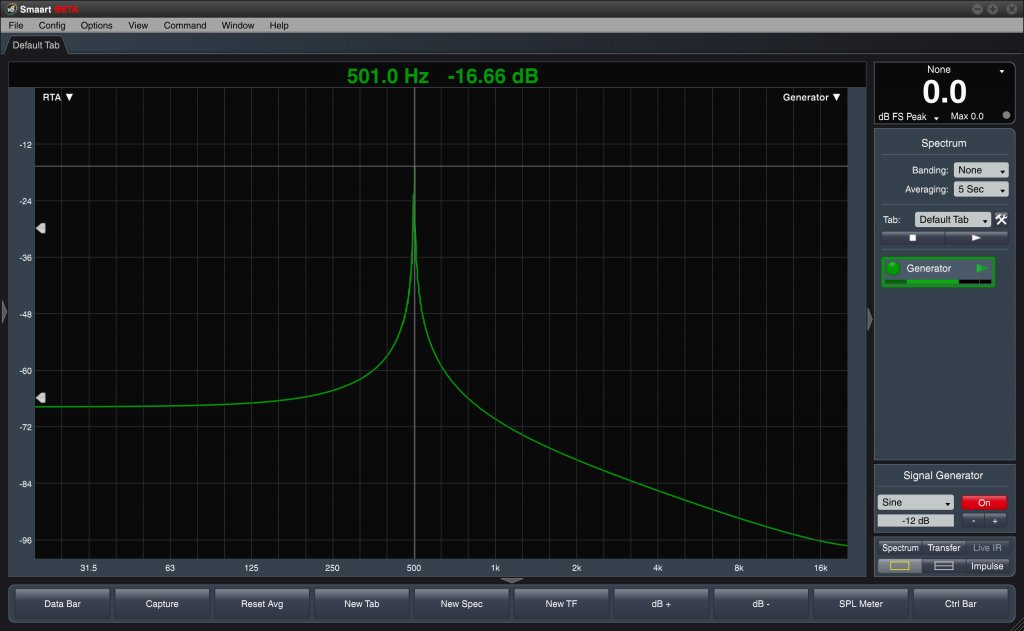
Enter the data window. If we “fade in” at the beginning out our selected signal chunk and “fade out” at the end, we’ve made the “infinitely repeating” assumption a lot more true because the end matches the beginning. That lets the DFT do its job with an input signal that matches its expectations. Here’s the same measurement taken with a data window applied:

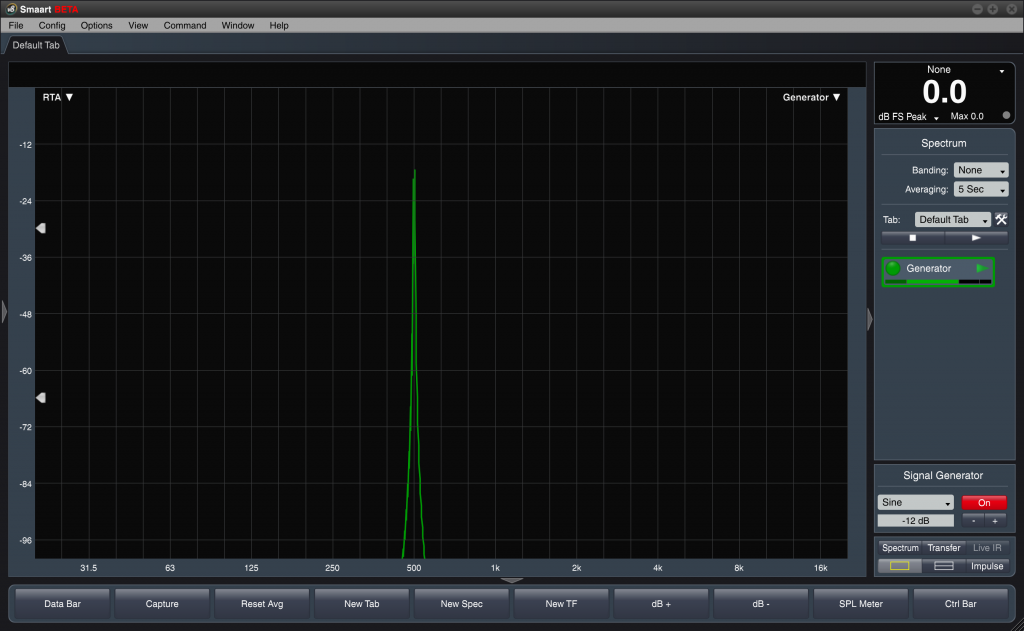
The spillage is greatly reduced, giving us a much cleaner measurement. There are a bunch of different data window options in Smaart, but the default settings were carefully chosen to give great results out of the box and shouldn’t require any tweaking in most situations. 

Time Record Length and Sampling Rate

Sample rate is measured in samples / second (or Hz), and the size of data chunks used for each FFT operation is measured in samples, but these are two different concepts.

As with any digital device, the highest frequency that the analyzer can resolve is dictated by the sampling rate of your audio interface. In broad terms, HF cutoff (known as the Nyquist frequency) will be about half the sampling rate. 

This concept should not be confused with the concept of FFT size, measured in samples. FFT size describes how many samples of data are used when calculating each frame of the measurement. Here’s the rule: In order to describe a frequency via FFT, the data window must be open long enough for that frequency to complete one full cycle.

That’s it! That’s beacuse the transform works something like this: For a 10ms time record, the transform says “Hey, input data. Who went through one cycle in this chunk of time? You! 100 Hz! What’s your magnitude? What’s your phase? Cool. Okay, next. Hey, who went through 2 cycles in this chunk of time? You! 200 Hz! What’s your magnitude? What’s your phase?” And so on. As long as the time window is open long enough for the frequency in question to make a full cycle, it’ll be included in our measurement.

“Smaart works by subtracting an electronic reference signal from an acoustic measurement signal”

A transfer function measurement compares two signals and shows the relationship between them. We use the terms Measurement signal and Reference signal, but both signals can be pretty much anything we want. By the time our signals get into the analyzer, they’re electronic signals that have been converted to digital, even if they were acoustic signals (sound wave) in a former life.

If you wanted to check that your two measurement microphones had matching responses, for example, you could place them nose to nose and take a transfer function measurement between them. (See this post for an example of that.) In that case, we have a comparative measurement between two microphone output signals. Or maybe you want to measure the response created by an equalizer or system processor by taking a transfer function measurement between the input and the output of the device.

Once you realize that the analyzer will try to compare any two signals we feed it, you can see how a transfer function measurement can be used for a lot of applications besides measuring the response of a loudspeaker in a room.

Loopback measurement delay

In a common configuration, we configure Smaart’s signal generator to output signal to two physical outputs on the audio interface. One is routed though the system we wish to measure, and the other is “looped back” to an input in the interface. In this way, we eliminate from the measurement any effects of computer / interface latency. The remaining time offset is a result of signal propagation through the system under test, not the latency of the computer-audio interface connection. In fact, that’s one of the reasons it’s not usually recommended to directly reference the internal signal generator – then you have driver latency and interface latency in the picture, and you can get into some real nasty situations. 

Coherence Trace

The coherence trace (not to be confused with the concept of phase coherence, which is something else) functions more or less as a data quality indicator, serving to indicate the level of correlation between the measurement and reference signals. In other words, “how confident can we be that the energy showing up at the mic was caused by our reference signal?” 

In order to avoid making decisions based on low-coherence data (the 60 Hz rumble caused by the PA or the subway under the theater should not be treated with EQ!) , Smaart’s coherence blanking threshold hides data whose coherence values fall below the threshold. This is a display-only feature, and has no effect on the underlying calculation. It only controls whether or not we paint those parts of the trace on the screen.