Deriving 6o6’s Lateral Aspect Ratio
Those studying the third edition of Bob “6o6” McCarthy’s system design treatise, Sound Systems: Design and Optimization, are introduced to a mechanism coined the Lateral Aspect Ratio. The basic idea is as follows:
The coverage angle of a loudspeaker is traditionally defined as the point as which, moving axially away from the on-axis reference, the high frequency coverage has decreased by 6 dB. However, as Bob points out, if the loudspeaker is projecting onto a flat listening area, such as a downward-firing ceiling speaker or a line of front fills across the front of a flat stage, this definition doesn’t tell us the whole story.
As we move laterally across the coverage area, we are losing level both axially and due to proximity, as we are getting further from the loudspeaker. Thus we will experience a 6 dB drop before we reach the angular off-axis edge. As is revealed by Figure 1 below, Point A is on axis to the loudspeaker at its reference depth, so we can consider this our 0 dB reference point. Point B is the same distance from the loudspeaker, and the -6 dB point that defines the loudspeaker’s coverage width.
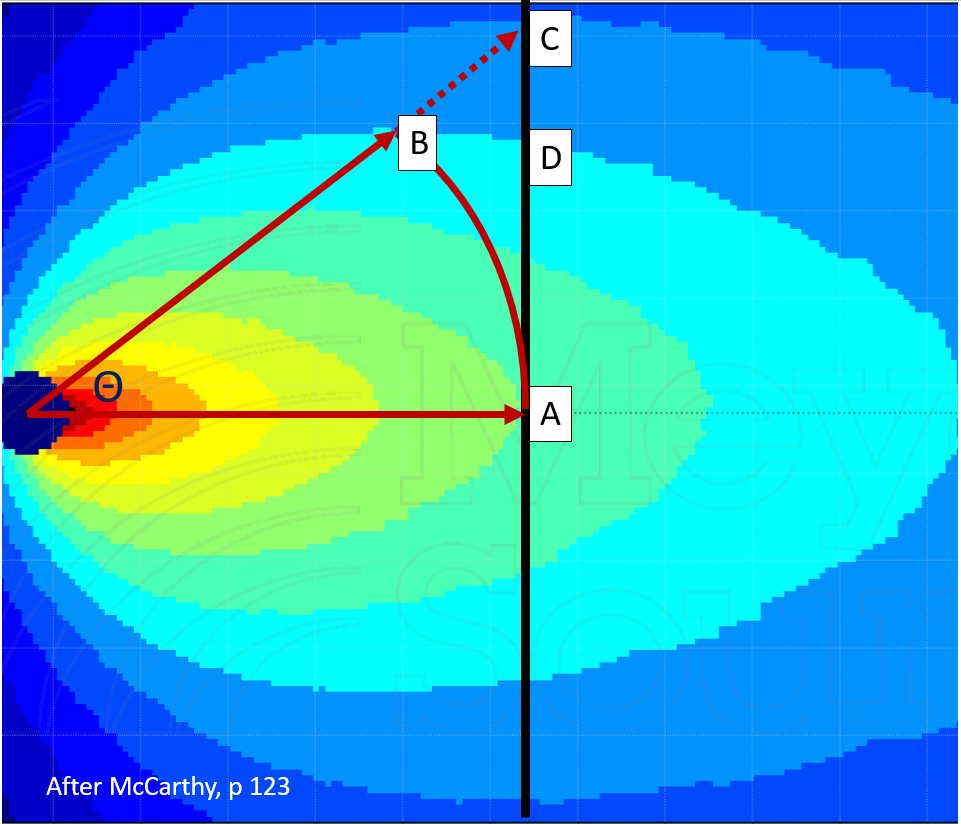
If one were using the common “protractor method” to determine proper front fill spacing, for example, one might erroneously use Point C as the -6 dB coverage edge based on moving laterally along the listening plane until reaching the loudspeaker’s off-axis angle. However, compared to the -6 dB we were experiencing at Point B, Point C suffers some additional loss because it is farther from the source, in addition to the same amount of angular loss. Therefore, the -6 dB point along the barricade happens sooner than we think (Point D).
The Lateral Coverage Angle metric describes the useable coverage angle of a loudspeaker when it is deployed in such a scenario, projecting onto a flat listening plane perpendicular to the loudspeaker. Once we take into account the additional loss incurred from moving further from the source as we move laterally, we can see that the loudspeaker has a narrower effective coverage angle due to the compounding losses (axial and distance). 6o6’s book contains a handy chart (Figure 3.41) allowing the reader to look up the Lateral Coverage Angle for loudspeakers of different dispersions (for example, a 90° loudspeaker has an effective Lateral Coverage Angle of 70°).
A related metric, and one that I find to be more useful in practical design work, is the Lateral Aspect Ratio. The LAR gives us the effective coverage width between -6 dB points for a given dispersion, as a function of throw distance. In other words, we can use it to figure out unity front fill spacing if we know how far the front fills need to throw to reach the barricade, and their dispersion. Referencing another handy chart (Figure 3.40), we can discover that the LAR for our 90° front fill is 1.41. If our front fills are throwing 10 feet to the nearest listener, we should space them at 10 x 1.41 = 14.1 feet apart to align their effective -6 dB edges.
Perhaps, like myself, you would choose to work through the underlying math that produces this value, such that in the field you can generate the LAR multiplier for loudspeakers of any dispersion, and be able to determine spacing without referencing a table. Today is your lucky day.
LAR = 2sin(Θ/2)
where Θ is the coverage angle of the loudspeaker.
Let’s look at the derivation. In Figure 2 below, T represents the throw distance of the loudspeaker, and since the coverage angle is determined by moving axially until we find the -6 dB point, we know that the outer edge of our coverage shape is by definition the same distance from the source, so that has a length of T as well. We’ll use W to indicate the width of the coverage shape.
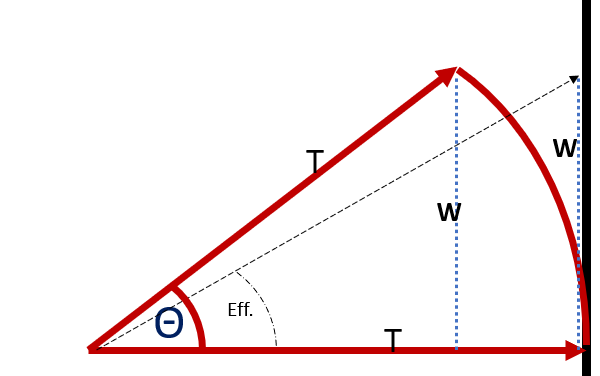
McCarthy’s LAR mechanism finds the coverage angle of the right triangle shape that has the same coverage depth (T) and the same lateral width (W). Since W would be considered the side opposite Θ, and T is the hypotenuse, we can find W with a little basic trig.
sin(Θ) = W/T
rearranging to solve for W:
W = Tsin(Θ)
This gives us the answer, but we’re not quite there = we’ve been looking at half the coverage angle of the entire loudspeaker, so in reality the entire coverage width (from -6 dB to – 6dB) is twice the value of W. So we want to add a coefficient of 2 to our formula to double the result. By similar logic, since we’ve been operating on half the coverage shape, Θ has been representing half the total coverage angle of the loudspeaker (45° for a 90° loudspeaker). When we use the formula in the field, we want to be able to simply plug in the loudspeaker’s dispersion, so we need to divide Θ by two.
Once more thing – we’re after a multiplier here. W is stated in terms of T, and we’re going to take the resulting value and multiply it by whatever the throw distance is, so we can normalize T to 1 for the purposes of this calculation.
With these changes, the formula becomes:
LAR = 2sin(Θ/2)
Let’s put it to practical use so we can see how it works. We have a 40′ wide stage, and it’s 7 feet from the stage lip to the first row of listeners along the barricade. Our front fill elements have a coverage angle of 100°. How far apart do we need to place them, and how many should we ask for?
LAR = 2sin(Θ/2)
LAR = 2sin(100/2)
LAR = 2sin(50)
LAR = 2(.7660)
LAR = 1.53
Multiply 1.53 times the throw distance of 7 feet to get a coverage width of 10.7 feet. Now we have our front fill spacing, and we’ve also learned we need four frontfill elements to cover the 40′ stage width.
One Reply to “Deriving 6o6’s Lateral Aspect Ratio”
Great! thanks! it took me some times to figured out when i read this book on the first time, i would also add to your article that since you explained the lateral coverage distance of a 100° speaker at 7feet we can also explain how to finde the useful coverage angle of 100° speaker with the help of : 2*arctan(Width/2/Depth) , with the Width = 10.7 and Depth = 7 the result would be = 74.78° (≈75°) as mentioned in the Figure 3.41 in the Book which is about 75% of the coverage angle.